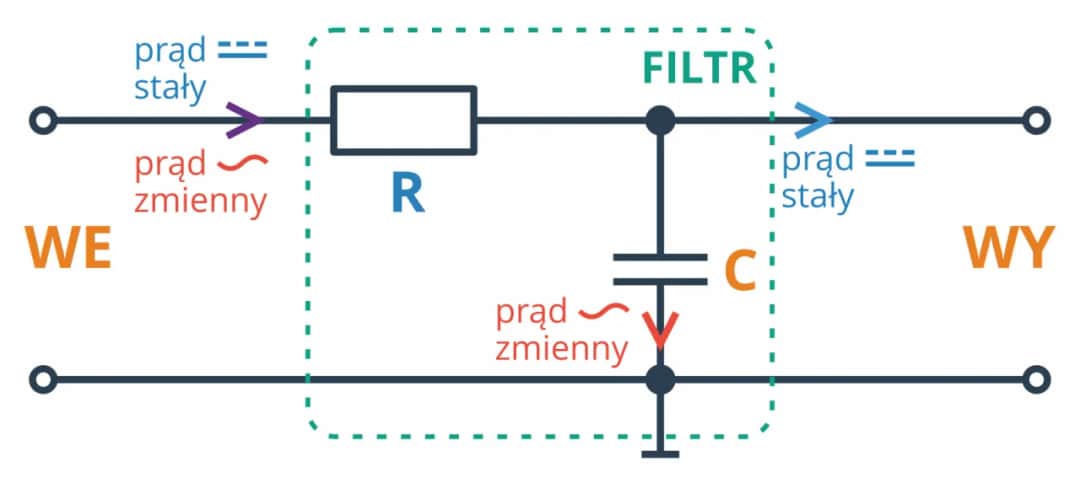
Filtr dolnoprzepustowy to podstawowy element układów elektronicznych, który przepuszcza sygnały o niskiej częstotliwości. Działa jak strażnik. Blokuje wysokie częstotliwości. Występuje w trzech głównych wariantach: RC, RL i LC. Każdy ma swoje unikalne cechy. Najprostszy i najczęściej stosowany to układ RC. Składa się tylko z rezystora i kondensatora. Filtry te są niezbędne w sprzęcie audio, telekomunikacji i przetwarzaniu sygnałów.
Najważniejsze informacje:- Filtr dolnoprzepustowy przepuszcza tylko sygnały poniżej częstotliwości granicznej
- Typ RC jest najprostszy i najczęściej używany w praktyce
- Częstotliwość graniczną oblicza się ze wzoru f = 1/(2πRC)
- Znajduje zastosowanie w sprzęcie audio i telekomunikacji
- Dostępne są różne kalkulatory online do projektowania filtrów
- Skutecznie eliminuje zakłócenia i szumy wysokoczęstotliwościowe
- Występuje w trzech podstawowych wariantach: RC, RL i LC
Zasada działania filtru dolnoprzepustowego
Filtr dolnoprzepustowy działa jak elektroniczne sito. Przepuszcza sygnały o niskiej częstotliwości, a blokuje te wysokie. Jest to podstawowy element układów elektronicznych służący do kształtowania charakterystyki częstotliwościowej sygnałów.
- Filtr RC - najprostszy układ złożony z rezystora i kondensatora, idealny do zastosowań audio.
- Filtr RL - wykorzystuje rezystor i cewkę, często stosowany w układach zasilających.
- Filtr LC - łączy cewkę i kondensator, zapewniając najlepszą charakterystykę tłumienia.
Projektowanie filtrów elektronicznych wymaga zrozumienia podstaw elektrotechniki. Te układy znajdują zastosowanie w sprzęcie audio, telekomunikacji i systemach przetwarzania sygnałów.
Kalkulator online do projektowania filtrów
Kalkulator filtrów RC to narzędzie znacznie upraszczające proces projektowania. Automatycznie oblicza parametry układu na podstawie wprowadzonych danych.
Interfejs kalkulatora filtra dolnoprzepustowego jest intuicyjny. Wystarczy wprowadzić wartości R i C. Program automatycznie generuje wykresy charakterystyki.
Wzory i obliczenia dla filtru RC
Obliczenia filtru dolnoprzepustowego opierają się na kilku kluczowych wzorach. Znajomość tych formuł pozwala zrozumieć działanie układu.
| Częstotliwość graniczna | fc = 1/(2πRC) |
| Napięcie wyjściowe | Vout/Vin = 1/√(1+(ωCR)²) |
Parametr R oznacza rezystancję w omach, C to pojemność w faradach. Częstotliwość graniczna fc określa punkt, w którym sygnał jest tłumiony o 3dB.
Jak dobrać wartości R i C?
Dobór elementów zaczyna się od określenia żądanej częstotliwości granicznej. Następnie można wybrać wartość jednego elementu i obliczyć drugi.
Praktyczne wartości R mieszczą się w zakresie 1kΩ do 100kΩ. Kondensatory najczęściej dobiera się z zakresu 100pF do 10µF.
Przykład obliczenia parametrów filtru
Załóżmy, że potrzebujemy filtr dolnoprzepustowy o częstotliwości granicznej 1kHz. Wybierzmy rezystor 10kΩ i obliczmy wymaganą pojemność kondensatora.
- Krok 1: Przekształcamy wzór fc = 1/(2πRC) na C = 1/(2πRfc)
- Krok 2: Podstawiamy wartości: C = 1/(2π × 10000Ω × 1000Hz)
- Krok 3: Otrzymujemy C ≈ 15.9nF (wybieramy standardową wartość 15nF)
Otrzymana wartość mieści się w typowym zakresie. Filtr z tymi parametrami zapewni skuteczne tłumienie sygnałów powyżej 1kHz.
Charakterystyka filtru w praktyce
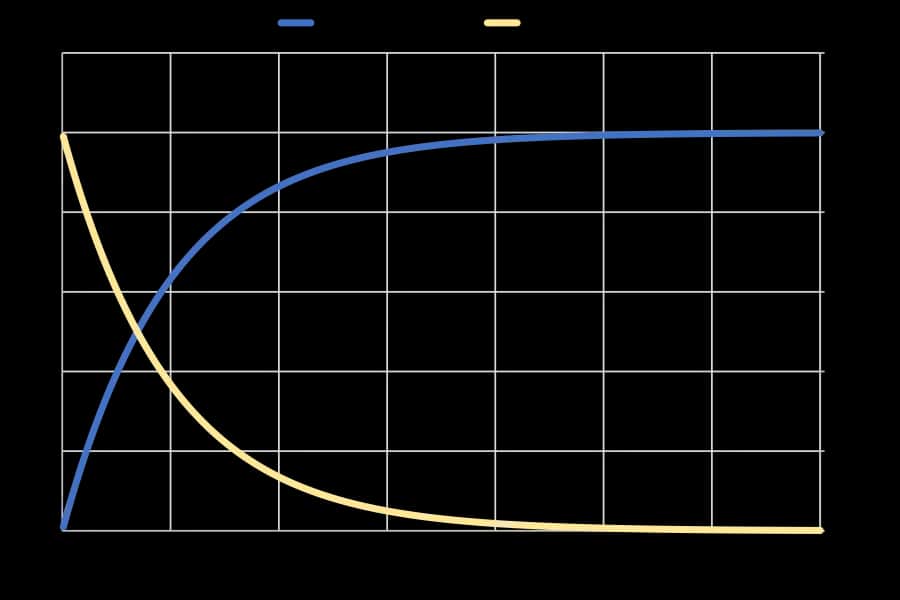
Charakterystyka filtru dolnoprzepustowego pokazuje jego rzeczywiste zachowanie. Spadek -20dB/dekadę występuje powyżej częstotliwości granicznej. Tłumienie zależy od częstotliwości sygnału wejściowego.
Ważna jest też faza sygnału. Przesunięcie fazowe rośnie wraz z częstotliwością. Przy fc wynosi dokładnie -45 stopni.
| Typ filtru | Nachylenie charakterystyki | Przesunięcie fazowe |
| RC | -20dB/dekadę | -45° przy fc |
| LC | -40dB/dekadę | -90° przy fc |
| Kaskada RC | -40dB/dekadę | -90° przy fc |
Analiza wykresów charakterystyki
Parametry filtrów dolnoprzepustowych najlepiej analizować na wykresach Bodego. Pokazują one amplitudę i fazę w funkcji częstotliwości w skali logarytmicznej.
Charakterystyka amplitudowa jest płaska poniżej fc. Pokazuje spadek -20dB/dekadę powyżej częstotliwości granicznej.
Wykres fazowy rozpoczyna się od 0°. Osiąga -45° przy fc i zmierza asymptotycznie do -90°.
Optymalizacja parametrów filtru
Optymalizacja zaczyna się od dokładnego określenia wymagań. Należy uwzględnić pasmo przepustowe, tłumienie i fazę.
Kluczowe jest dobranie standardowych wartości elementów. Można użyć równoległego lub szeregowego połączenia komponentów.
Czasem warto zastosować kaskadę filtrów. Zwiększa to nachylenie charakterystyki.
Wpływ temperatury i tolerancji elementów
Temperatura wpływa na parametry elementów. Rezystory mają typowo tolerancję 1-5%, kondensatory nawet 20%.
Warto uwzględnić najgorszy przypadek. Częstotliwość graniczna może się zmienić o kilka-kilkanaście procent.
Testowanie zaprojektowanego filtru
Testowanie rozpoczyna się od pomiarów napięcia wyjściowego. Należy sprawdzić charakterystykę przy różnych częstotliwościach. Pomiary porównujemy z obliczeniami.
Ważna jest też odpowiedź na skok jednostkowy. Pokazuje zachowanie filtru w dziedzinie czasu.
Wyniki testów powinny mieścić się w założonych granicach. Typowa tolerancja częstotliwości granicznej to ±10%.
Praktyczne zastosowanie filtrów dolnoprzepustowych
Filtry dolnoprzepustowe to fundamentalne układy w elektronice. Ich projektowanie wymaga zrozumienia kilku kluczowych zasad. Najważniejsza jest częstotliwość graniczna, która determinuje punkt podziału między sygnałami przepuszczanymi a tłumionymi.
Proces projektowania znacznie ułatwia kalkulator filtrów dolnoprzepustowych. Dobór wartości R i C nie musi być skomplikowany. Wystarczy trzymać się standardowych wartości i pamiętać o tolerancjach elementów. Najczęściej stosowany układ RC sprawdza się w większości zastosowań.
Testowanie i optymalizacja to ostatnie, ale kluczowe etapy. Należy zawsze weryfikować charakterystykę filtru w praktyce. Pomiary powinny uwzględniać wpływ temperatury i tolerancji elementów. W razie potrzeby można zastosować kaskadę filtrów dla uzyskania lepszych parametrów tłumienia.